POSETTE 2025 is a wrap! 🎁 Thanks for joining the fun. Missed it? Watch all 42 talks online.
The first distributed database that I worked on was called CSPIT. The project was led by a visionary architect and involved some of the smartest developers I knew at Amazon.
CSPIT never saw the light of day. On the technical side, we ran into scalability issues for two reasons. In these posts, I intend to share those two battle-hardened lessons that cost us years of developer time to learn. Of course, these learnings aren't enough to build a distributed database, but hopefully there's enough in them to save you notable time in building distributed systems.
The first learning is about a theoretical understanding of which computations are easy to scale. Taking a step back, you can solve all distributed systems problems in one of two ways (we already knew this):
- Bringing the data to the computation
- Bringing the computation to the data
As an example, let's say that you keep your sales data in a distributed datastore, and you want to know your total revenue. One can answer this simple question in one of two ways. I'm expressing the question in SQL below, but the idea applies to any query language.
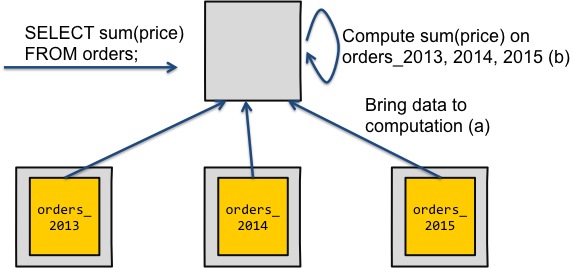
The first diagram has the benefit that it's simple. You can express any computation by pulling all data to a particular node, and then running the original query on this data. Of course, the drawback is that this method doesn't quite scale. For one, you're issuing a lot of network I/O during the data transfer, and network is your least scalable resource. For another, you aren't parallelizing any of the work, and instead running the entire computation on a single node.
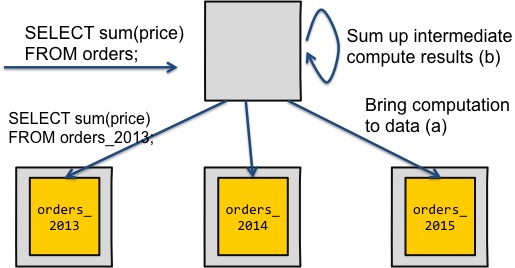
The second diagram solves these two scalability issues. We're both parallelizing the computation here, and are also only transferring computation results over the network. We had to do a final sum on the coordinator node, but that was simple enough.
Now, let's look at a slightly more complex computation. Say, we're looking to compute the average order value. In this case, can we ask each worker node to compute their averages, and then average those out?
No, we can't run averages on worker nodes, and then average those out. We need to have each worker node compute their sum(order_value) and count(order_value), and then sum(sum()) / sum(count()) on the coordinator node. This was a simple transformation, but why did we need to do it now?
In other words, why is the sum query easier to parallelize than the average one? Because one computation is commutative by its nature, and the other one isn't. (a + b = b + a ; a / b ≠ b / a). [1]
When you're pushing your computations to your data, you're in fact transforming your computations in to their commutative form. Still, how exactly does this observation help me build my distributed database?
If you're building a database, you probably have a query language that expresses each query in some logical form. The commutativity property will hold and help with any well defined language. Below, I'll pick SQL as an example language for two reasons. SQL has wide adoption, and we at Citus have experience in scaling it out.
SQL uses relational algebra to express a query. When you send a query to your database, that query gets parsed and converted into a logical query tree. For example, if your query has a Where clause in it, that's a Filter node in the query tree. If the query has an aggregate function, that gets expressed as an Extended Operator node in the tree.
The mapping from SQL to relational algebra, and relational algebra operators have been discussed and studied in detail. We therefore won't dive into those details and will instead focus on using these algebra operators in the context of distributed systems. Let's start by looking at an example SQL query.
SELECT sum(price) FROM orders, nation
WHERE orders.nation = nation.name AND
orders.date >= '2012-01-01' AND
nation.region = 'Asia';
This simple query joins the sales table with a small nation table to select rows that meet a particular criteria. The query then computes total sales volume across selected rows. Now, let's take a look at the distributed logical query plan for this query.
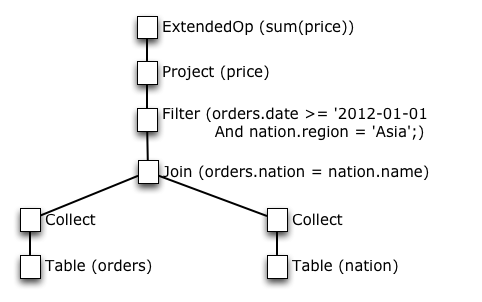
At a first glance, this query tree looks like a standard relational algebra node tree. [2] If you look closely however, you'll note one difference. The query tree has two Collect nodes near its leaves. This new operator type collects the data underneath it into a single machine.
Tying this back to the beginning of our blog post, these Collect nodes pull the two tables' data to one location. The rest of the query tree then executes the join, filtering, and computation on this collected data.
But we already know that doesn't scale. Let's now put together our knowledge on scaling network I/O, commutative operations, and relational algebra. Does the Collect operator commute with the Filter operator? Yes. Great, let's pull the Collect up.
In fact, there's a simple way to optimize this logical plan: pull up Collect nodes and push down computation nodes in the tree, as long as the commutative and distributive properties hold. [3] The following diagram shows the logical query plan once we apply these optimizations.
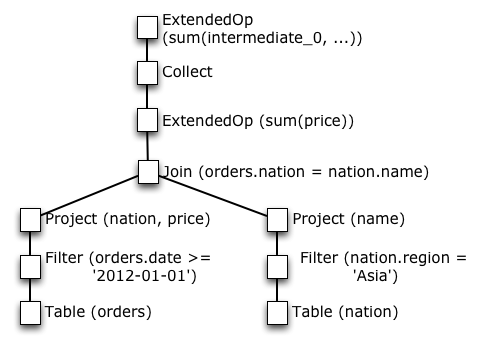
This optimized plan has many computations pushed down in the query tree, and only collects a small amount of data. This enables scalability. Much more importantly, this logical plan formalizes how relational algebra operators scale in distributed systems, and why.
That's one key takeaway I had from building a distributed database before. In the land of distributed systems, commutativity is king. Model your queries with respect to the king, and they will scale.
Of course, there's more to building a distributed database than just having the right logical plan. If you're interested in databases as an end user, please try CitusDB out. We have our v4.0 coming up next month, and we'd love to hear your take. If you're looking to build your own distributed database instead, we hope you find this blog post helpful. Drop us a line, and we'd be happy to chat! Also, we had a second key learning that we intend to share that in an upcoming blog post.
[1] We're using the + operator and the sum() aggregate function interchangeably to be brief in this post. In fact, those two operations are related, but have different representations in distributed relational algebra.
[2] A second difference is that all distributed operators in these logical plans can operate on one or multiple fragments of data.
[3] The Join node is a binary operator. Therefore, we use the distributive property when optimizing query plans that involve the join node.
